Kalman Filter
- Overview
- State Estimation Using Kalman Filter
- Implementation Approach
- Overcoming Unforeseen Obstacles During Implementation
- Resources
It is common for sensors to have some degree of noise in the data they record, meaning the measured values may differ from the true or actual values. The goal for this project was to implement a Kalman filter to reduce noise in simulated sensor data, providing a more accurate representation of the true value.
In this simulation, a car model can be controlled to drive around a plane while its velocity is sampled. To simulate the noise that typically exists in a sensor, a random value scaled by a noise factor (allowing for control over the amount of noise) is added to the sampled velocity.
private Vector3 GetVelocityData()
{
// Return velocity data from sensor or other source
Vector3 velocity = rb.linearVelocity + new Vector3(UnityEngine.Random.Range(-1f, 1f) * sensorNoiseFactor,
UnityEngine.Random.Range(-1f, 1f) * sensorNoiseFactor,
UnityEngine.Random.Range(-1f, 1f) * sensorNoiseFactor);
return velocity;
}The noisy velocity data is then processed by a Kalman filter class, which calculates the filtered velocity. Using a set of 3x3 input matrices, the Kalman filter determines how much weight to assign to the noisy velocity versus a predicted velocity generated by the input model.
As explained in the video Visually Explained: Kalman Filters 1 and in the second chapter of Introduction and Implementations of the Kalman Filter 2, a Kalman filter is an estimation algorithm that combines predictions from a model with noisy observations to continuously estimate the state of a dynamic system. It recursively updates a set of state estimates based on a combination of the predicted state and the observed measurements. The predictions are weighted based on the uncertainty associated with both the model and the measurements, and the filter continually adjusts these weights based on the latest observations.
Mathematical Concepts:
- Kalman Gain Matrix: determines how much of the new measurement information should be used to update the predicted state estimate. It is used to weigh the relative contributions of the predicted state estimate and the observed measurements.
- Measurement Noise Matrix: describes the amount of noise present in the measurements provided by the sensor. The more noise, the less the measurement is used to update the state.
- State Vector: since the only state variable is a Vector3 velocity, the state vector would simply be a Vector3 that holds the velocity in each direction.
- Measurement Matrix: since the state variable is only velocity, the measurement matrix would be a row vector that maps the velocity to the measurement space.
- Measurement Space Matrix: the set of all possible values that a measurement can take. Since our sensor can measure any range of values, and the only state variable is velocity, the measurement Matrix should be [1.0]
Predict Function:
// Prediction step
public void Predict()
{
// Update State:
// this is the predicition.
state = stateTransition * state + controlMatrix * controlVector;
// Update Covariance:
// covariance represents the uncertainty or error in the estimated state of the system
covariance = stateTransition * covariance * stateTransition.Transpose() + processNoise;
}Update Function:
public void Update(Vector3 measurement)
{
// Kalman Gain:
// The Kalman gain determines how much of the new measurement information
// should be used to update the predicted state estimate. It is used to weigh
// the relative contributions of the predicted state estimate and the observed measurements.
// MeasurementNoise:
// describes the amount of noise present in the measurements provided by the sensor.
// The more noise, the less the measurement is used to update the state.
Matrix3x3 kalmanGain = covariance * measurementMatrix *
(covariance * measurementMatrix * measurementMatrix + measurementNoise).Invert();
// State Vector:
// Since the only state variable is a Vector3 velocity, the state vector
// would simply be a Vector3 that holds the velocity in each direction.
// MeasurementMatrix:
// Since the state variable is only velocity, the measurement matrix would
// be a row vector that maps the velocity to the measurement space.
// MeasurementSpace:
// the set of all possible values that a measurement can take.
// Since our sensor can measure any range of values, and the only state
// variable is velocity, the measureMatrix should be [1.0]
// Therefore the Vector3 multiplied by the kalmanGain would be the
// measurement velocity minus the previous state
// [velocity.x] [state.x]
// [velocity.y] - [1.0] * [state.y]
// [velocity.z] [state.z]
//Vector3 kalman = kalmanGain * (measurement - measurementMatrix * state);
// Update state
state = state + (kalmanGain * (measurement - measurementMatrix * state));
// Update covariance
covariance = (Matrix3x3.identity - kalmanGain * measurementMatrix) * covariance;
}Analyzing Efficiency:
The efficiency of the Kalman filter can be evaluated by its ability to estimate the state of a dynamic system with increasing accuracy and precision as more measurements are processed.
Initially, the uncertainty in the state estimate may be high due to limited data. However, as the filter processes additional measurements, it converges to a more accurate estimate of the true state. This is achieved by calculating a weighted sum of the prior estimate and the measurement, where the weights are dynamically adjusted based on the covariance matrices of the prior estimate and the measurement.
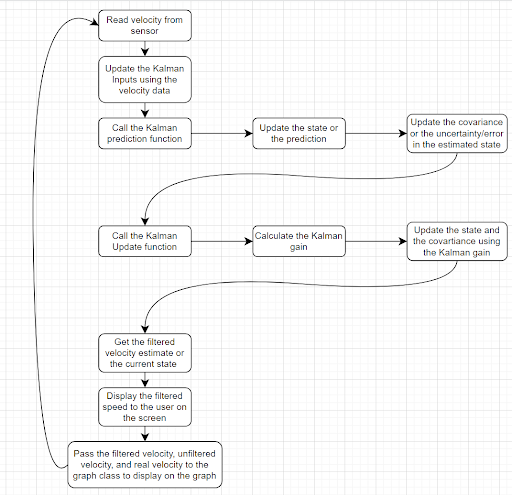
To simulate a sensor update interval, a timer is updated each frame. If the timer is equal to or exceeds the update interval, the timer is reset and the velocity data is sampled. When the velocity data is sampled, the following steps are performed:
- Update the Kalman inputs using the velocity data (set the F,B,Q,H,R matrices and control vector)
- Perform the prediction step
- Perform the update step with the velocity measurement
- Get the filtered velocity estimate
- Use filtered velocity estimate to update a graph of the velocity over time
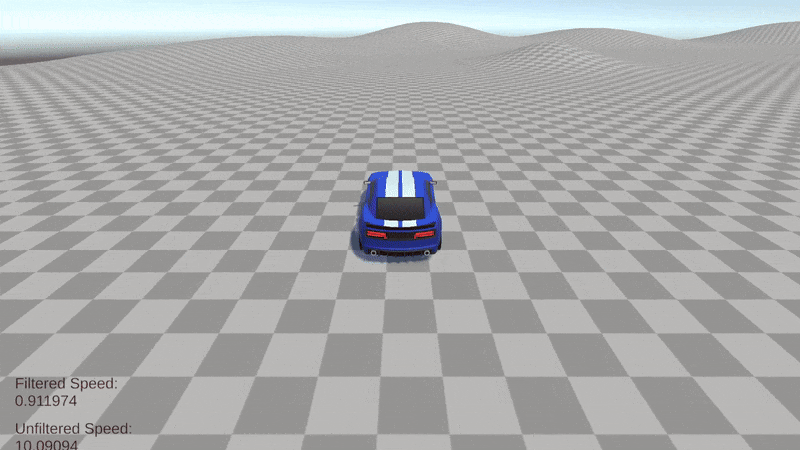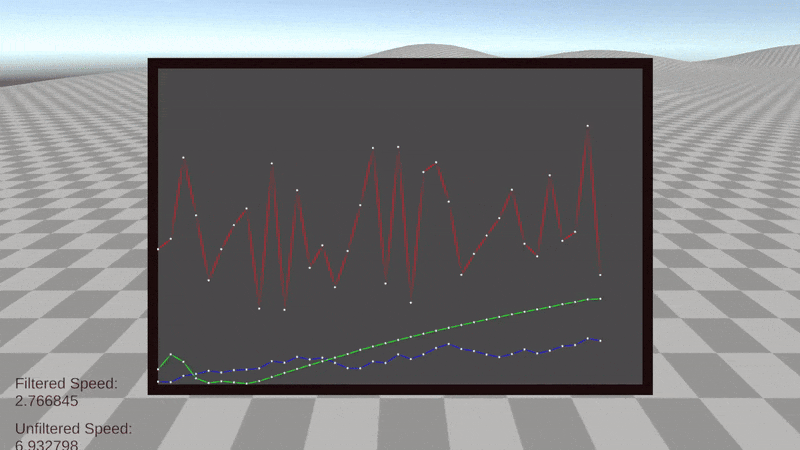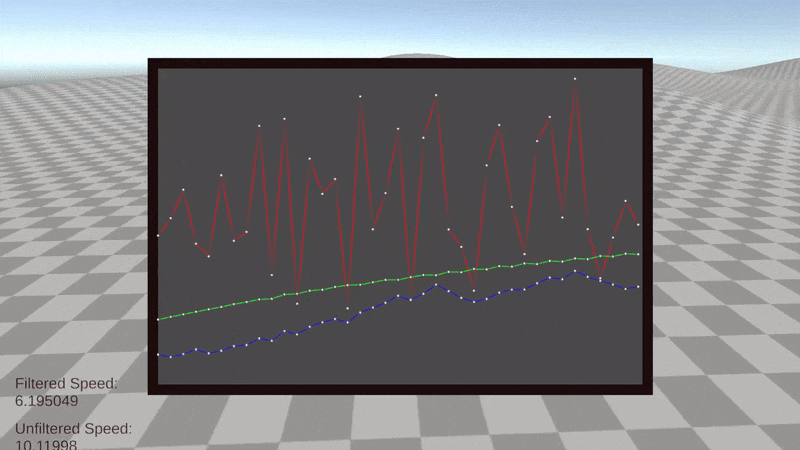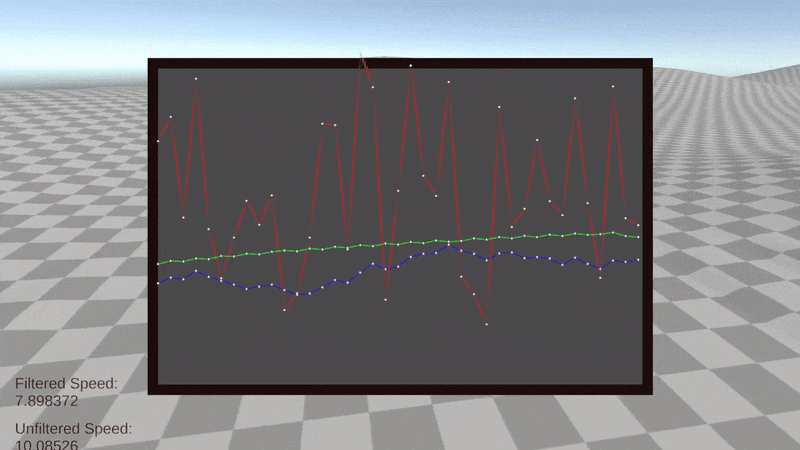
Pressing the tab key during the play state will display a graph of the velocity over time. The interval on the x-axis corresponds to the sensor update interval.
- The red line represents the noisy unfiltered velocity.
- The green line represents the true velocity.
- The blue line represents the filtered velocity.

Flow Chart:
One issue during implementation was defining a control matrix (B) and control vector to accurately predict the car’s velocity. The issue lies with the complexity of vehicle dynamics models and the fact that the code Unity uses for determining a rigidbody’s velocity is not publicly available. These factors combined resulted in a significant challenge in providing an accurate model for the Kalman filter. Here is the model that I came up with that focuses on accurately predicting linear acceleration. There are still some flaws in the model, which is why the filtered velocity doesn’t always seem to match the real velocity. Perhaps a better model could be created using a machine learning algorithm, such as a Hidden Markov Model, to better capture the system dynamics.
public void GetControl()
{
float width = collider.size.x;
float height = collider.size.y;
float depth = collider.size.z;
float A = 2 * (width * height + width * depth + height * depth);
float wheelRadius = wheelCollider.radius;
float wheelWidth = wheelRadius * 2f * Mathf.PI / wheelCollider.forwardFriction.extremumSlip;
float friction = wheelCollider.forwardFriction.extremumValue;
float slip = wheelCollider.forwardFriction.extremumSlip;
float rollingResistanceCoefficient = friction * wheelRadius / (wheelWidth * slip);
dragForce = 0.5f * airDensity * rb.linearDamping * Mathf.Pow(GetVelocityData().magnitude, 2) * A;
rollingResistance = rollingResistanceCoefficient * rb.mass;
dragForce += rollingResistance;
if (Mathf.Abs(rb.linearVelocity.magnitude) < 0.1f)
{
acceleration = 0f;
}
else
{
acceleration = (carController.motorTorque - dragForce) / rb.mass;
}
// local space vector
controlVector = new Vector3(sensorUpdateInterval * Mathf.Cos(carController.currentSteerAngle) * acceleration,
0,
sensorUpdateInterval * Mathf.Sin(carController.currentSteerAngle) * acceleration);
// world space vector
controlVector = gameObject.transform.TransformVector(controlVector);
Matrix3x3 B;
if (useControlMatrix)
{
B = new Matrix3x3(1, 0, 0,
0, 1, 0,
0, 0, 1);
}
else
{
B = new Matrix3x3(0, 0, 0,
0, 0, 0,
0, 0, 0);
}
kalmanFilter.SetControlVector(controlVector);
kalmanFilter.SetControlMatrix(B);
}